Using T-SQL for Finding Narrowing Ranges of Data

By: Tim Smith   |   Updated: 2017-10-18   |   Comments   |   Related: > TSQL

Problem

We use chart trends in data to identify our best guesses for pricing products for our clients and adjusting these prices as we receive feedback. We've recently converted our environment to a SQL Server environment and wanted to know if we could use a tool like T-SQL to identify price ranges in graphs including support in terms of response from buyers, or resistance in terms of no response from buyers to assist our clients.

Solution

In this tip, we'll look at considering a narrow set of values for a range, which may indicate a trend on a chart. This is meant as a tool to combine with other statistical analysis, such as trendslines, and not a standalone tool of looking at data. As an example, we'll look at determining a lower range for a 3-4 month period (business days only). When we look at top or bottom ranges, we should consider the following for querying the data:

1. The time range we want to identify a range. In this tip's example, we'll look at values over a 3-4 month period of time.
2. The percent range of higher, middle or lower values. Do we want to look at the bottom 1%, 3%, 5%, etc. In this tip on each query, we'll be looking at the bottom 10%, but on other data sets we may want to use a lower or higher percent of ranges from our measuring point.
3. The deviation of the range we've chosen in point two compared with the average. Stated in an algorithm: the standard deviation of [x]% of values divided by the average, with the result multiplied by 100 to express it as a percent. In an example where we take 5% of the highest values from a table of 1 million records:

--If we had a data set of 1 million values, and we were looking at the highest 5% of these values that would be a total of 50,000 data points:
SELECT 
 AVG(Value) AvgValue --Average of the 50,000 highest values
 , STDEV(Value) StDevValue --Standard deviation of the 50,000 highest values
 , ((STDEV(Value)/AVG(Value))*100) StDevPercentAvg --Algorithm stated as a T-SQL query
FROM tblFiftyK ---- where this table has the 50,000 highest values

The last point might matter in some industries or situations where we want to narrow (or expand) a data set due to the volatile nature of data - such as the example of some clothing selling better in the summer season versus the winter season. Using contrived data sets in T-SQL, in the below examples we see the impact of a data set that jumps from one extreme value to another extreme value compared to a data set with a narrow range of values (body temperature):

CREATE TABLE StDevJump(
 Value INT
)

INSERT INTO StDevJump VALUES (20)
INSERT INTO StDevJump VALUES (1)
INSERT INTO StDevJump VALUES (21)
INSERT INTO StDevJump VALUES (2)
INSERT INTO StDevJump VALUES (20)
INSERT INTO StDevJump VALUES (1)
INSERT INTO StDevJump VALUES (22)
INSERT INTO StDevJump VALUES (3)
INSERT INTO StDevJump VALUES (20)
INSERT INTO StDevJump VALUES (1)

SELECT 
 AVG(Value) AvgValue --11
 , STDEV(Value) StDevValue --10.049323
 , ((STDEV(Value)/AVG(Value))*100) StDevPercentAvg --91.357480
FROM StDevJump

DROP TABLE StDevJump


CREATE TABLE StDevFever(
 Value DECIMAL(5,2)
)

INSERT INTO StDevFever VALUES (98.6)
INSERT INTO StDevFever VALUES (98.5)
INSERT INTO StDevFever VALUES (98.6)
INSERT INTO StDevFever VALUES (98.7)
INSERT INTO StDevFever VALUES (98.5)
INSERT INTO StDevFever VALUES (98.6)
INSERT INTO StDevFever VALUES (98.6)
INSERT INTO StDevFever VALUES (98.5)
INSERT INTO StDevFever VALUES (98.6)
INSERT INTO StDevFever VALUES (98.7)
INSERT INTO StDevFever VALUES (98.6)
INSERT INTO StDevFever VALUES (98.6)
INSERT INTO StDevFever VALUES (98.7)
INSERT INTO StDevFever VALUES (98.5)
INSERT INTO StDevFever VALUES (98.6)
INSERT INTO StDevFever VALUES (98.5)
INSERT INTO StDevFever VALUES (98.6)
INSERT INTO StDevFever VALUES (98.5)
INSERT INTO StDevFever VALUES (101)

SELECT 
 AVG(Value) AvgTemp --98.710526
 , STDEV(Value) StDevTemp --0.558664
 , ((STDEV(Value)/AVG(Value))*100) StDevPercentAvg --0.565962
FROM StDevFever

DROP TABLE StDevFever

The results are printed out in comments next to the queries and in the first example we, we see a data set with a standard deviation that is over 91% compared to its average - a standard deviation that is 10 when the average is 11. In the second example, the standard deviation isn't even one percent compared to its average. Why this matters is that we would want to consider broad ranges in data in some cases, like finding a top or bottom range in a fashion season (or cycle). If I see a standard deviation that is a large percent of an average value - such as greater than 3 percent, I will further investigate the data, as this may require a broad or narrower measurement point in terms of filtering the time.

The first step in our example will be creating a table and importing a data set where we will use the 10 percent of lowest values. download this csv file and execute the below in SQL Server, only changing where the file is pointing to if the file exists in a different location:

CREATE TABLE tblImport(
 DateField SMALLDATETIME,
 ValueField DECIMAL(13,4)
)

BULK INSERT tblImport
FROM 'C:\ETLFiles\Import\imp.csv'
WITH (
 FIELDTERMINATOR = ','
 ,ROWTERMINATOR = '0x0a'
 , FIRSTROW=2
)

CREATE CLUSTERED INDEX IX_DateField ON tblImport (DateField)

SELECT *
FROM tblImport

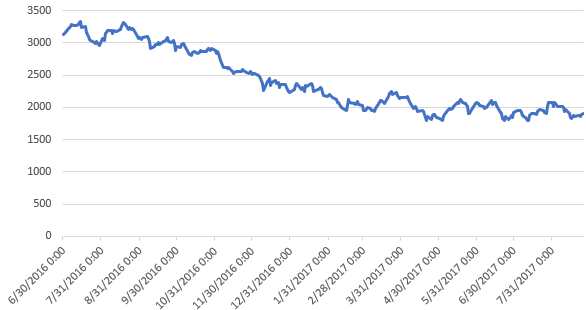
The above graph shows these values visually. Next, we want to evaluate the lowest 10% of values (you can use the TOP PERCENT or TOP 9 - in this tip, I use the actual number for simplicity) and compare the standard deviation in these values to the average expressed as a percent, as mentioned in the above section:

DECLARE @startdate DATETIME
SELECT @startdate = MAX(DateField) FROM tblImport

;WITH TestStDev AS(
 SELECT TOP 9 ValueField
 FROM tblImport
 WHERE DateField > DATEADD(DD,-93,@startdate)
 ORDER BY ValueField ASC
)
SELECT ((STDEV(ValueField)/AVG(ValueField))*100) Deviation
FROM TestStDev

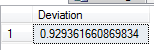
As we see, the result is low, which means for this example, we can use this range of values without further investigation - unless we found that to be too high. How high or low you want the deviation to be depends on the data set; as we saw in the above example with fever, a range of 3 would be too high - deviation with fever should be less than 1 (if 98.6 is normal and 99 is fever, we don't want a broad deviation, like 3). For these data, 3 will function for our tip, and one could argue that a range of 10-20 would also function. For this tip, I'll use this part as a filtering point for this data set - provided that it's below 3, I'll continue getting the values:

DECLARE @startdate DATETIME
SELECT @startdate = MAX(DateField) FROM tblImport

;WITH TestStDev AS(
 SELECT TOP 9 ValueField
 FROM tblImport
 WHERE DateField > DATEADD(DD,-93,@startdate)
 ORDER BY ValueField ASC
)
SELECT @test = ((STDEV(ValueField)/AVG(ValueField))*100)
FROM TestStDev

---- This will be used in the next step; the query only proceeds if it's within our acceptable range.
IF (@test < 3)
BEGIN
 ---- Evaluation
END

Next, we'll look at the average of the lower 10% of values (using an approximate number like the TOP 9 for 93 values). In the below code, we can see this and I recommend executing the query both within the CTE (uncomment the parameter) and as a whole:

DECLARE @startdate DATETIME
SELECT @startdate = MAX(DateField) FROM tblImport

;WITH Sup90 AS(
  --DECLARE @startdate DATETIME
  --SELECT @startdate = MAX(DateField) FROM tblImport
  SELECT TOP 9 ValueField
  FROM tblImport
  WHERE DateField > DATEADD(DD,-93,@startdate)
  ORDER BY ValueField ASC
 )
 SELECT AVG(ValueField) NinetyThreeDay
 FROM Sup90

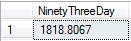
For this 93 measurement range, these are the lowest 10% of values and we see the average of those values. Returning to the initial steps - we are choosing this time range to evaluate if we're near the lower range of values. This time range depends - we may choose to look over a year, or several years, and we may choose five or six measuring points instead of three.

Next, we'll look at the 62 and 31 measurement points (in the below saved in variables @60 and @30) and the below code shows each query independently so that you can call the query within the CTE if you want to evaluate each set of values independently:

DECLARE @startdate DATETIME
SELECT @startdate = MAX(DateField) FROM tblImport

DECLARE @test DECIMAL(10,6)
;WITH TestStDev AS(
 SELECT TOP 9 ValueField
 FROM tblImport
 WHERE DateField > DATEADD(DD,-93,@startdate)
 ORDER BY ValueField ASC
)
SELECT @test = ((STDEV(ValueField)/AVG(ValueField))*100)
FROM TestStDev


IF (@test < 3)
BEGIN
 DECLARE @90 DECIMAL(13,4), @60 DECIMAL(13,4), @30 DECIMAL(13,4)
 ;WITH Sup90 AS(
  SELECT TOP 9 ValueField
  FROM tblImport
  WHERE DateField > DATEADD(DD,-93,@startdate)
  ORDER BY ValueField ASC
 )
 SELECT @90 = AVG(ValueField)
 FROM Sup90

 ;WITH Sup60 AS(
  SELECT TOP 6 ValueField
  FROM tblImport
  WHERE DateField > DATEADD(DD,-62,@startdate)
  ORDER BY ValueField ASC
 )
 SELECT @60 = AVG(ValueField)
 FROM Sup60

 ;WITH Sup30 AS(
  SELECT TOP 3 ValueField
  FROM tblImport
  WHERE DateField > DATEADD(DD,-31,@startdate)
  ORDER BY ValueField ASC
 )
 SELECT @30 = AVG(ValueField)
 FROM Sup30

 SELECT 
  @90 AS NinetyThreeDay
  , @60 AS SixtyTwoDay
  , @30 AS ThirtyOneDay
  , @90 - @30 AS NinetyThreeThirtyOneDayDiff
  , @90 - @60 AS NinetyThreeSixtyTwoDayDiff
  , @60 - @30 AS SixtyTwoThirtyOneDayDiff

END

The final query compares the average values returned in the 93, 62, and 31 measuring points. What we find is that both the ninety-third and sixty-second measuring point values are less than the thirty-first measuring point value. Since the difference between the 93 and 62nd measuring point differ the least by amount (when using the absolute value of all measurements), we can conclude that lower range of values can be seen between this period of time. This does not mean that data may stay in this range and that the data won't fall to lower values - it only means that for this period of data, this is the lowest range. Depending on your needs for finding a range - whether the range is the upper, lower or middle range - you can use this range to fit your needs. For a buyer, a low range might be a time to buy; for a seller, a high range might be a time to sell; for a researcher, this may help you identify patterns that validate or invalidate your theories.

Next Steps

• Before looking at ranges, consider the data set, time range that you'll be filtering, and the deviation of the values compared to the average of those values within the data set.
• Always consider cycles with data: for an example, weather comes in cycles, so when identifying support or resistance patterns, we can use the cycles as accurate time filters, or filters for identifying when a pattern becomes unusual. On graphs, consider graphs on a smaller cycle, medium cycle and large cycle. Excel is one tool that you can use for easily building a graph, or else you can use tools like R, Tableau, or SSRS.
• Use caution when using standards or best practices that exclude exceptions. When read in the context of statistical applications, the philosophic work The Power of the Powerless by Vaclav Have makes a strong point against overlooking exceptions. An exception can change normal, such as an exception like Bill Gates impacting billions of people with software tools that change "normal" indefinitely. Exceptions are not rules by definition, but this doesn't mean they lack importance, especially in the context of business.

About the author

Tim Smith works as a DBA and developer and also teaches Automating ETL on Udemy.

This author pledges the content of this article is based on professional experience and not AI generated.

View all my tips