By: Eli Leiba | Updated: 2020-10-29 | Comments (4) | Related: > TSQL
Problem
This tip addresses the problem of solving any set of three linear equations with three unknown values (x, y, z) by using the N determinants mathematics method. In this tip I will describe a way to implement this with SQL Server's T-SQL code.
The format of the linear equations set is assumed like this:
- A1x + B1y + C1z = Y1
- A2x + B2y + C2z = Y2
- A3x + B3y + C3z = Y3
Where A1, B1, C1, Y1, A2, B2, C2, Y2, A3, B3, C3, Y3 are real numbers.
The T-SQL code will find the solution for the set of equations by finding the values of x, y, z.
If there is no solution these output arguments will contain NULL as the output.
Solution
My solution involves creating a T-SQL stored procedure in the SQL Server master database, (or any other user database) called dbo.usp_solve_linear_equation_set_for_3_unkowns that accepts the input of 12 real arguments: A1, B1, C1, Y1, A2, B2, C2, Y2, A3, B3, C3, Y3 and also 3 output arguments X, Y, Z and computes the solution.
Note: The mathematical theory that the T-SQL is based on is taken from the following article: Linear Equations: Solutions Using Determinants with Three Variables.
The solution involves calculating 4 results: DET, DETX, DETY, DETZ
The determinant of coefficients defined as:
DET = (a1 * b2 * c3 + a2 * b3 * c1 + a3 * b1 * c2) – (c1 * b2 * a3 + c2 * b3 * a1 + c3 * b1 * a2);
The determinant of X (all occurrences of Ai replace by Yi)
DETX = (y1 * b2 * c3 + y2 * b3 * c1 + y3 * b1 * c2) – (c1 * b2 * y3 + c2 * b3 * y1 + c3 * b1 * y2);
The determinant of Y (all occurrences of Bi replace by Yi)
DETY = (a1 * y2 * c3 + a2 * y3 * c1 + a3 * y1 * c2) – (c1 * y2 * a3 + c2 * y3 * a1 + c3 * y1 * a2);
The determinant of Z (all occurrences of Ci replace by Yi)
DETZ = (a1 * b2 * y3 + a2 * b3 * y1 + a3 * b1 * y2) – (y1 * b2 * a3 + y2 * b3 * a1 + y3 * b1 * a2);
If DET equals zero, then no solution exists, the T-SQL code encounters a division by zero exception and the output results is NULL for all output arguments.
If DET does not equal zero then a solution exists and is as follows:
X = DETX / DET Y = DETY / DET Z = DETZ / DET
SQL Server Stored Procedure
Here is the implementation in a T-SQL stored procedure:
-- ====================================================================================
-- Author: Eli Leiba
-- Create date: 04-10-2020
-- Description: Solves 3 linear equations set
-- The result is the real values for x, y and z unknowns (if solution exists)
-- if no solution exists the values are set to NULL
-- ====================================================================================
SET ANSI_NULLS ON
GO
SET QUOTED_IDENTIFIER ON
GO
CREATE PROCEDURE [dbo].[usp_solve_linear_equation_set_for_3_unkowns]
(@a1 real, @b1 real, @c1 real, @y1 real,
@a2 real, @b2 real, @c2 real, @y2 real,
@a3 real, @b3 real, @c3 real, @y3 real,
@x real out, @y real out, @z real out)
AS
BEGIN
DECLARE @det REAL = 0;
DECLARE @detx REAL = 0;
DECLARE @dety REAL = 0;
DECLARE @detz REAL = 0;
BEGIN TRY
SET @det = (@a1 * @b2 * @c3 + @a2 * @b3 * @c1 + @a3 * @b1 * @c2) –
(@c1 * @b2 * @a3 + @c2 * @b3 * @a1 + @c3 * @b1 * @a2);
SET @detx = (@y1 * @b2 * @c3 + @y2 * @b3 * @c1 + @y3 * @b1 * @c2) –
(@c1 * @b2 * @y3 + @c2 * @b3 * @y1 + @c3 * @b1 * @y2);
SET @dety = (@a1 * @y2 * @c3 + @a2 * @y3 * @c1 + @a3 * @y1 * @c2) –
(@c1 * @y2 * @a3 + @c2 * @y3 * @a1 + @c3 * @y1 * @a2);
SET @detz = (@a1 * @b2 * @y3 + @a2 * @b3 * @y1 + @a3 * @b1 * @y2) –
(@y1 * @b2 * @a3 + @y2 * @b3 * @a1 + @y3 * @b1 * @a2);
SET @x = @detx / @det;
SET @y = @dety / @det;
SET @z = @detz / @det;
END TRY
BEGIN CATCH
SET @x = NULL
SET @y = NULL
SET @z = NULL
END CATCH
END
GO
Sample Stored Procedure Execution
Here is an example that we will use with the stored procedure to solve for x, y and z:
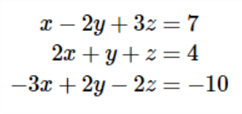
This is how the stored procedure is called. For any value that is just the variable, we will use a value of 1 as shown below.
use master
go
declare @x real, @y real, @z real
exec dbo.usp_solve_linear_equation_set_for_3_unkowns
1, -2, 3, 7,
2 , 1, 1, 4,
-3, 2, -2, -10,
@x out, @y out, @z out
print @x
print @y
print @z
And the output for the solution is as follows:
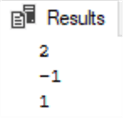
x = 2; y = -1; z = 1
We can then plug in the values for x, y and z to check the equation:
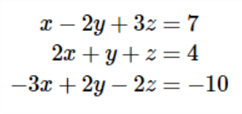
2 - 2 * (-1) + 3 * 1 = 7 2 * 2 - 1 + 1 = 4 -3 * 2 + 2 * (-1) - 2 * 1 = - 10
Next Steps
- You can create and compile this stored procedure in any database you choose in order to solve any three linear equations set.
- The procedure was tested for SQL Server 2019, but should work with all versions of SQL Server.
About the author
Eli Leiba is a senior application DBA, a teacher and a senior database consultant with 19 years of RDBMS experience.This author pledges the content of this article is based on professional experience and not AI generated.
View all my tips
Article Last Updated: 2020-10-29
