SQL Server Logarithmic Functions LOG() and LOG10() for Data Outliers

By: Harris Amjad | Updated: 2022-10-20 | Comments (2) | Related: > Functions System

Problem

Logarithmic functions are essential functions and can be very useful for data analysis. During data analysis, we often find that a particular column has some outliers. Outliers can have a significant impact on statistical outcomes, which results in incorrect interpretations. Moreover, eliminating the outlier from the data results in data loss, hence discarding this solution. In this case, logarithmic functions can help solve the skewness caused due to the few outliers in the data. This tip will guide you on how to use the logarithmic functions in SQL Server.

Solution

A logarithmic function (y = log_a) is the inverse of the exponential function (y = a^x). In Microsoft SQL Server, there are two logarithmic functions.

LOG()
LOG10()

LOG() – Syntax

The LOG() function returns the natural logarithm of a number or the number's logarithm to the specified base. Following is the syntax of the LOG().

--number is required
--base is optional
LOG(number, base)

The number is the required field for this function. Its value must be greater than 0. However, the base is an optional field. If the value of the base is not provided, then this function calculates the natural logarithm of a number. In the case of the natural logarithm, the base is, by default, e (Euler's Number or Exponential Constant). If the base value is provided, it must be greater than 1.

Let's jump into different examples of LOG().

LOG() – Examples

Example 1: Calculate the LOG() of the positive integer without base (natural logarithm).

--number positive integer
--base omitted
SELECT 'LOG(10)' as [Function], LOG(10) as Result

Example 2: Calculate the LOG() of the positive floating point without base (natural logarithm).

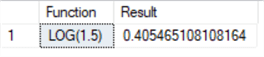
--number positive floating point
--base omitted
SELECT 'LOG(1.5)' as [Function], LOG(1.5) as Result

Example 3: Calculate the LOG() of the negative integer without base (natural logarithm).

--number negative integer
--base omitted
SELECT 'LOG(-10)' as [Function], LOG(-10) as Result

Example 4: Calculate the LOG() of the negative floating point without base (natural logarithm).

--number negative floating point
--base omitted
SELECT 'LOG(-1.5)' as [Function], LOG(-1.5) as Result

Example 5: Calculate the LOG() of the one without base (natural logarithm).

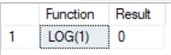
--number 1
--base omitted
SELECT 'LOG(1)' as [Function], LOG(1) as Result

Example 6: Calculate the LOG() of the positive integer with a positive integer base.

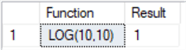
--number positive integer
--base positive integer
SELECT 'LOG(10,10)' as [Function], LOG(10,10) as Result

Example 7: Calculate the LOG() of the negative integer with a negative integer base.

--number negative integer
--base negative integer
SELECT 'LOG(-10,-10)' as [Function], LOG(-10,-10) as Result

Example 8: Calculate the LOG() of the positive integer with a negative integer base.

--number positive integer
--base negative integer
SELECT 'LOG(10,-10)' as [Function], LOG(10,-10) as Result

Example 9: Calculate the LOG() of the negative integer with a positive integer base.

--number negative integer
--base positive integer
SELECT 'LOG(-10,10)' as [Function], LOG(-10,10) as Result

Example 10: Calculate the LOG() of the positive floating point with a positive floating point base.

--number positive floating point
--base positive floating point
SELECT 'LOG(10.1,1.5)' as [Function], LOG(10.1,1.5) as Result

LOG10() – Syntax

The LOG10() function returns the logarithm of a number to the base 10. Following is the syntax of the LOG10().

--number is required
LOG10(number)

The number is the required field for this function. Its value must be greater than 0. However, the base is fixed at 10 in this function.

Let's jump into different examples of LOG10().

LOG10() – Examples

Example 1: Calculate the LOG10() of a positive integer.

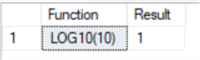
--number positive integer
SELECT 'LOG10(10)' as [Function], LOG10(10) as Result

Example 2: Calculate the LOG10() of a positive floating point.

--number positive floating point
SELECT 'LOG10(1.5)' as [Function], LOG10(1.5) as Result

Example 3: Calculate the LOG10() of a negative integer.

--number negative integer
SELECT 'LOG10(-10)' as [Function], LOG10(-10) as Result

Example 4: Calculate the LOG10() of a negative floating point.

--number negative floating point
SELECT 'LOG10(-1.5)' as [Function], LOG10(-1.5) as Result

Example 5: Calculate the LOG10() of one.

--number 1
SELECT 'LOG10(1)' as [Function], LOG10(1) as Result

Example 6: Calculate the LOG10() of zero.

--number 0
SELECT 'LOG10(0)' as [Function], LOG10(0) as Result

Logarithmic Function – Grocery Store Sales Example

As discussed earlier, logarithmic scaling can help solve the skewness in the data. The skewness is due to the significant variance between the data points. Skewness means that a couple of data points are above or below the normal range of the values. Hence, these data points will disturb the overall analysis. In this case, logarithmic functions help to scale all the data points in a way that will suppress the impact of outliers on the comprehensive dataset.

Let's consider the grocery store sales example to illustrate how logarithmic scaling can help accurately interpret yearly sales.

Logarithmic Function – Grocery Store Sales Schema

The following will be used to create a table and insert values:

CREATE TABLE GroceryStoreSales (
   [id] int identity(1,1) not null Primary Key,
   [year] int,
   [sales_in_USD] int
);
--not providing id value since its auto generated
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2000,9000);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2001,9100);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2002,9220);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2003,9030);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2004,9045);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2005,25000);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2006,8500);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2007,10000);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2008,9800);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2009,9345);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2010,9122);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2011,8500);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2012,9220);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2013,9900);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2014,9290);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2015,9630);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2016,9145);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2017,3600);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2018,7540);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2019,10500);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2020,6000);
INSERT INTO GroceryStoreSales([year], sales_in_USD) VALUES (2021,17000);

Logarithmic Function – Grocery Store Sales Analysis

In the data we just created, let's consider the normal range of value for sales to be $8000-$10500. And the value that does not lie in that range is considered the outlier. The following image shows the table along with the outliers highlighted.

Table along with the outliers highlighted

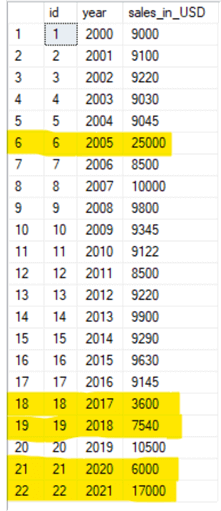
Now let's take the natural logarithm of the sales_in_USD column. For calculating the natural logarithm following is the query.

select *,
LOG(sales_in_USD) as [log_of_sales_in_USD]
from GroceryStoreSales

I have highlighted the known outliers to show the values for the LOG function.

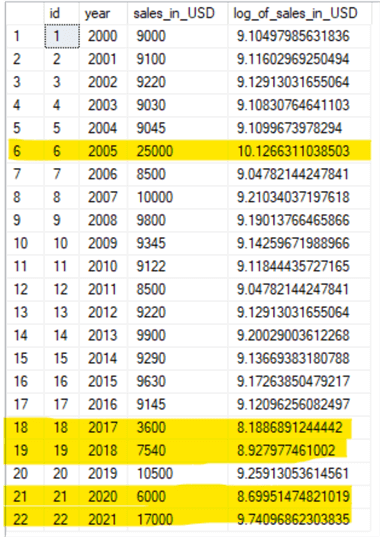
The table above shows that the outliers' difference is vast from the normal value range in the actual sales_in_USD column. However, this difference is significantly reduced when we apply the natural logarithm. Hence, during analysis, the logarithmic scale will have less impact on the trend than the actual sales_in_USD.

Similarly, let's try taking the LOG10() for the same column. Following is a query to calculate the LOG10() for the sale_in_USD column.

select *,
LOG(sales_in_USD) as [log_of_sales_in_USD],
LOG10(sales_in_USD) as [log10_of_sales_in_USD]
from GroceryStoreSales

Again, I have highlighted the known outliers to show the values for the LOG10 function.

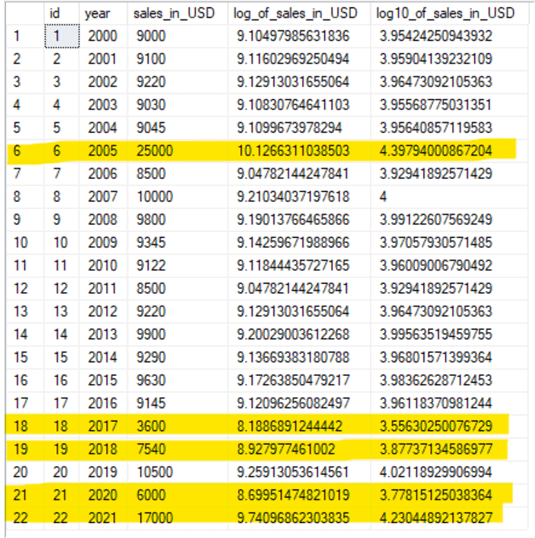
Calculate the LOG10() for the sale_in_USD column

In the case of LOG10(), the difference from the normal value range is reduced even more. Hence, using LOG10() in this scenario proves more accurate.

Summary

In a dataset, we often come across outliers. One possible solution is to delete the outliers completely. But, this solution will result in loss of data and most of the time we don't want to lose the data. Moreover, when we plot that column with the outliers then our trend/analysis will be faulty. In this case, the LOG function comes into play.

The LOG function helps in scaling the data in the entire column (column that contains the outliers) in such a way that impact of outliers is minimized. So if we take the LOG of the column (column with outliers) then we need not to ignore any value in the dataset. The idea is that taking the log of the data can restore symmetry to the data.

For comparison, in sales_in_USD column we can see the outliers have a very huge difference from the nominal range. However, when we apply the LOG of that column with a different base the outlier difference from nominal log value range goes very down. Let's consider row number 6. The actual sales_in_USD value is 25000; 14500 (25000-10500) is the difference from nominal value. However, if we see log_of_sales_in_USD for 25000 it is 10.126; 0.876 (log(25000)-log(10500)) is the difference from the nominal value range. It can be observed that the difference has been cut greatly if we take the LOG of the sales_in_USD column. As a result of this, if we plot log_of_sales_in_USD instead of sales_in_USD column then we can have a better picture and better analysis, because outliers will not be misleading for the entire analysis.

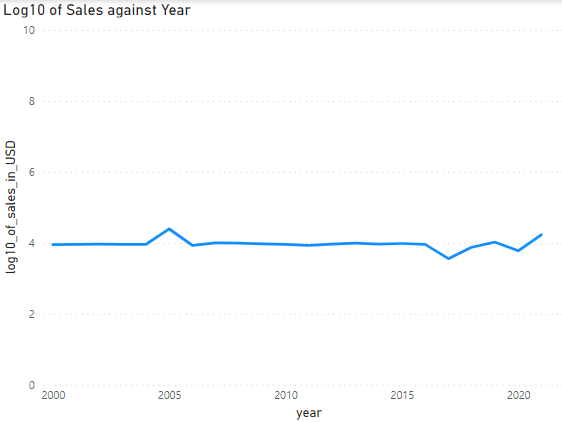
Here is the data plotted on graphs to help visualize.

Here is the data using the sales amount.

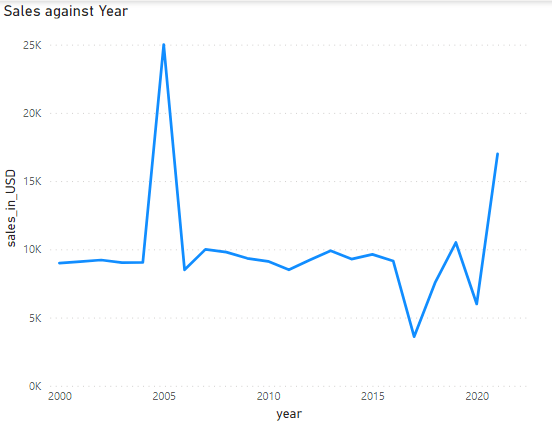
Here is the data using the LOG values.

Here is the data using the LOG10 values.

Conclusion

This tip highlights the syntax and the different examples of logarithmic functions in SQL Server. Moreover, it discusses the use case where the logarithmic function can improve the overall analysis. From the grocery store sales example, it can be seen that we can test the logarithmic function with different base values to get the optimal base value. There are many other analysis use cases where this mathematical function can help.

Next Steps

For details related to other SQL server functions.

About the author

Harris Amjad is a BI Artist, developing complete data-driven operating systems from ETL to Data Visualization.

This author pledges the content of this article is based on professional experience and not AI generated.

View all my tips

Article Last Updated: 2022-10-20

Data Analysis with SQL Server Logarithmic Functions LOG() and LOG10()